I am doing some SfM and having troubles getting R and T from the essential matrix.
Here is what I am doing in sourcecode:
Mat fundamental = Calib3d.findFundamentalMat(object_left, object_right);
Mat E = new Mat();
Core.multiply(cameraMatrix.t(), fundamental, E); // cameraMatrix.t()*fundamental*cameraMatrix;
Core.multiply(E, cameraMatrix, E);
Mat R = new Mat();
Mat.zeros(3, 3, CvType.CV_64FC1).copyTo(R);
Mat T = new Mat();
calculateRT(E, R, T);
where `calculateRT` is defined as follows:
private void calculateRT(Mat E, Mat R, Mat T) {
/*
* //-- Step 6: calculate Rotation Matrix and Translation Vector
Matx34d P;
//decompose E
SVD svd(E,SVD::MODIFY_A);
Mat svd_u = svd.u;
Mat svd_vt = svd.vt;
Mat svd_w = svd.w;
Matx33d W(0,-1,0,1,0,0,0,0,1);//HZ 9.13
Mat_<double> R = svd_u * Mat(W) * svd_vt; //
Mat_<double> T = svd_u.col(2); //u3
if (!CheckCoherentRotation (R)) {
std::cout<<"resulting rotation is not coherent\n";
return 0;
}
*/
Mat w = new Mat();
Mat u = new Mat();
Mat vt = new Mat();
Core.SVDecomp(E, w, u, vt, Core.DECOMP_SVD); // Maybe use flags
Mat W = new Mat(new Size(3,3), CvType.CV_64FC1);
W.put(0, 0, W_Values);
Core.multiply(u, W, R);
Core.multiply(R, vt, R);
T = u.col(2);
}
And here are the results of all matrizes after and during calculation.
Number matches: 10299
Number of good matches: 590
Number of obj_points left: 590.0
CameraMatrix:
[1133.601684570312, 0, 639.5;
0 , 1133.601684570312, 383.5;
0, 0, 1]
DistortionCoeff: [0.06604336202144623; 0.21129509806633; 0; 0; -1.206771731376648]
Fundamental:
[4.209958176688844e-08, -8.477216249742946e-08, 9.132798068178793e-05;
3.165719895008366e-07, 6.437858397735847e-07, -0.0006976204595236443;
0.0004532506630569588, -0.0009224427024602799, 1]
Essential:
[0.05410018455525099, 0, 0;
0, 0.8272987826496967, 0;
0, 0, 1]
U: (SVD)
[0, 0, 1;
0, 0.9999999999999999, 0;
1, 0, 0]
W: (SVD)
[1; 0.8272987826496967; 0.05410018455525099]
vt: (SVD)
[0, 0, 1;
0, 1, 0;
1, 0, 0]
R:
[0, 0, 0;
0, 0, 0;
0, 0, 0]
T:
[1; 0; 0]
And for completion here are the image I am using: left and right.
Before calulation of FeaturePoints and so on, I am doing an undistrortion of the images.
Can someone point out where something is goind wrong or what I am doing wrong?
edit: Question
Is it possible that my fundamental matrix is equals to the essential matrix as I am in the calibrated situation and Hartley and zissermann says:
„11.7.3 The calibrated case:
In the case of calibrated cameras normalized image coordinates may be used, and the essential matrix E computed instead of the fundamental matrix”
I've found the misstake. This code is not doing the right matrix multiplication.
Mat E = new Mat();
Core.multiply(cameraMatrix.t(),fundamental, E);
Core.multiply(E, cameraMatrix, E);
I changed this to
Core.gemm(cameraMatrix.t(), fundamental, 1, cameraMatrix, 1, E);
which is now doing the right matrix multiplication. As far as I can get ir from the documentation, Core.multiply is doing the multiplication for each element. not the dot product of row*col.
First, unless you computed the fundamental matrix by taking explicitly into account the inverse of the camera matrix, you are not in the calibrated case, hence the fundamental matrix you estimate is not an essential matrix. This is also quite easy to test: you just have to eigen-decompose the fundamental matrix and see whether the two non-zero eigen-values are equal (see § 9.6.1 in Hartley&Zisserman's book).
Second, both the fundamental matrix and the essential matrix are defined for two cameras and do not make sense if you consider only one camera. If you do have two cameras, with respective matrices K1 and K2, then you can obtain the essential matrix E12, given the fundamental matrix F12 (which maps points in I1 to lines in I2), using the following formula (see equation 9.12 in Hartley&Zisserman's book):
E12 = K2T . F12 . K1
In your case, you used K2 on both sides.
Related
I have a question where I represent a graph in terms of a 2D array.
I have a sample as well, but I have no idea, how it works....
This is the graph I am given
And this is how they represent it using a 2D array
How does one translate to the other?
Also, this is a part of an implementation of Dijsktra's algorithm.
Here is the code for your reference, it is taken from
geeksforgeeks
// A Java program for Dijkstra's single source shortest path algorithm.
// The program is for adjacency matrix representation of the graph
import java.util.*;
import java.lang.*;
import java.io.*;
class ShortestPath {
// A utility function to find the vertex with minimum distance value,
// from the set of vertices not yet included in shortest path tree
static final int V = 9;
int minDistance(int dist[], Boolean sptSet[])
{
// Initialize min value
int min = Integer.MAX_VALUE, min_index = -1;
for (int v = 0; v < V; v++)
if (sptSet[v] == false && dist[v] <= min) {
min = dist[v];
min_index = v;
}
return min_index;
}
// A utility function to print the constructed distance array
void printSolution(int dist[])
{
System.out.println("Vertex \t\t Distance from Source");
for (int i = 0; i < V; i++)
System.out.println(i + " \t\t " + dist[i]);
}
// Function that implements Dijkstra's single source shortest path
// algorithm for a graph represented using adjacency matrix
// representation
void dijkstra(int graph[][], int src)
{
int dist[] = new int[V]; // The output array. dist[i] will hold
// the shortest distance from src to i
// sptSet[i] will true if vertex i is included in shortest
// path tree or shortest distance from src to i is finalized
Boolean sptSet[] = new Boolean[V];
// Initialize all distances as INFINITE and stpSet[] as false
for (int i = 0; i < V; i++) {
dist[i] = Integer.MAX_VALUE;
sptSet[i] = false;
}
// Distance of source vertex from itself is always 0
dist[src] = 0;
// Find shortest path for all vertices
for (int count = 0; count < V - 1; count++) {
// Pick the minimum distance vertex from the set of vertices
// not yet processed. u is always equal to src in first
// iteration.
int u = minDistance(dist, sptSet);
// Mark the picked vertex as processed
sptSet[u] = true;
// Update dist value of the adjacent vertices of the
// picked vertex.
for (int v = 0; v < V; v++)
// Update dist[v] only if is not in sptSet, there is an
// edge from u to v, and total weight of path from src to
// v through u is smaller than current value of dist[v]
if (!sptSet[v] && graph[u][v] != 0 && dist[u] != Integer.MAX_VALUE && dist[u] + graph[u][v] < dist[v])
dist[v] = dist[u] + graph[u][v];
}
// print the constructed distance array
printSolution(dist);
}
// Driver method
public static void main(String[] args)
{
/* Let us create the example graph discussed above */
int graph[][] = new int[][] { { 0, 4, 0, 0, 0, 0, 0, 8, 0 },
{ 4, 0, 8, 0, 0, 0, 0, 11, 0 },
{ 0, 8, 0, 7, 0, 4, 0, 0, 2 },
{ 0, 0, 7, 0, 9, 14, 0, 0, 0 },
{ 0, 0, 0, 9, 0, 10, 0, 0, 0 },
{ 0, 0, 4, 14, 10, 0, 2, 0, 0 },
{ 0, 0, 0, 0, 0, 2, 0, 1, 6 },
{ 8, 11, 0, 0, 0, 0, 1, 0, 7 },
{ 0, 0, 2, 0, 0, 0, 6, 7, 0 } };
ShortestPath t = new ShortestPath();
t.dijkstra(graph, 0);
}
}
If this is the graph given to me, for example, how would I represent it using a 2D array?
You can read it like a coordinate table.
Every row represents a single vertex and every column value on the same row represents the distance to the Nth vertex.
Examples:
0, 1: first row, second column has the value of 4; which means vertex 0's distance to vertex 1 is 4.
1, 7: second row, 8th column has the value of 11; which means vertex 1's distance to vertex 7 is 11.
And so on...
They have used an adjacency matrix to represent an weighted undirected graphs. According to geeksforgeeks:
Adjacency Matrix: Adjacency Matrix is a 2D array of size V x V where V is the
number of vertices in a graph. Let the 2D array be adj[][], a slot adj[i][j] = 1
indicates that there is an edge from vertex i to vertex j. Adjacency matrix for
undirected graph is always symmetric. Adjacency Matrix is also used to represent
weighted graphs. If adj[i][j] = w, then there is an edge from vertex i to vertex
j with weight w.
As the last two line state, adjacency matrix can be used to store a weighted graph which they have done in this case.
There might be few problems if you use adjacency matrix to represent weighted graphs. Here we use 0 to represent no-edge between any two vertices. If there is any graph which has a weight 0in the graph, then a little change in the adjacency matrix will be needed since 0 already represents no-edge.
In the comments you mention about another graph. That one, however, is not weighted. It is also not undirected graph since its not symmetric.
Do comment if you have any other doubts.
I think I've figured it out!
In the example graph, there are 9 vertices. Therefore a 9x9 2D matrix is created, such that:
Row 1 corresponds to vertex 0, Row 2 corresponds to vertex 1 and so on
and
Column 1 corresponds to vertex 0, Column 2 corresponds to vertex 1 and so on
and the array is filled such that it contains the weight of the edges between node x and y. For example: Row 1 column 2 (map0) contains the weight of the edge between vertex 0 and vertex 1.
Therefore for a graph with n vertices, an nxn array needs to be created such that the location[x][y] in the array contains the weight between edge from x to y.
As for the example graph I had asked the solution for, this would be its corresponding 2D Matrix:
It is a little big, because we create a 16x16 2D matrix
I am trying to determine a way to change the pixel color of my masks from black to a different color. Unfortunately, I have not be able to determine a way to do this task. Essentially, what I am trying to do is take this image:
and convert the black portions to a color with values (255, 160, 130). I have tried several methods to try and achieve my goal. These include draw contours, setTo, and looping through the matrix. Unfortunately all of these attempts have failed. I have included the code and the resulting outcomes below.
Draw Contours method
System.loadLibrary(Core.NATIVE_LIBRARY_NAME);
Mat img = Imgcodecs.imread(
"C:\\Users\\Hassan\\Documents\\School\\Me\\COMP5900 Y\\Project\\Project\\src\\resources\\face.jpg");
Mat img_grey = new Mat();
Mat grad = new Mat(), grad_x = new Mat(), grad_y = new Mat();
Mat abs_grad_x = new Mat(), abs_grad_y = new Mat();
int ddepth = CvType.CV_32F;
int scale = 1;
int delta = 0;
Imgproc.GaussianBlur(img, img, new Size(3, 3), 0, 0, Core.BORDER_CONSTANT);
Imgproc.cvtColor(img, img_grey, Imgproc.COLOR_BGR2GRAY);
// Apply Sobel
Imgproc.Sobel(img_grey, grad_x, ddepth, 1, 0, 3, scale, delta, Core.BORDER_DEFAULT);
Imgproc.Sobel(img_grey, grad_y, ddepth, 0, 1, 3, scale, delta, Core.BORDER_DEFAULT);
// converting back to CV_8U
Core.convertScaleAbs(grad_x, abs_grad_x);
Core.convertScaleAbs(grad_y, abs_grad_y);
// Total Gradient (approximate)
Core.addWeighted(abs_grad_x, 0.5, abs_grad_y, 0.5, 0, grad);
Photo.fastNlMeansDenoising(grad, grad);
Imgproc.GaussianBlur(grad, grad, new Size(3, 3), 0, 0, Core.BORDER_CONSTANT);
// isolate background
Mat background = new Mat();
Imgproc.threshold(grad, background, 2, 255, Imgproc.THRESH_BINARY);
// draw contours
List<MatOfPoint> contours = new ArrayList<>();
Mat hierarchy = new Mat();
Imgproc.findContours(background, contours, hierarchy, Imgproc.RETR_TREE, Imgproc.CHAIN_APPROX_NONE);
Mat drawing = Mat.zeros(background.size(), CvType.CV_8UC3);
List<MatOfPoint> hullList = new ArrayList<>();
for (MatOfPoint contour : contours) {
MatOfInt hull = new MatOfInt();
Imgproc.convexHull(contour, hull);
Point[] contourArray = contour.toArray();
Point[] hullPoints = new Point[hull.rows()];
List<Integer> hullContourIdxList = hull.toList();
for (int i = 0; i < hullContourIdxList.size(); i++) {
hullPoints[i] = contourArray[hullContourIdxList.get(i)];
}
hullList.add(new MatOfPoint(hullPoints));
}
for (int i = 0; i < contours.size(); i++) {
Scalar color = new Scalar(255, 160, 130);
Imgproc.drawContours(drawing, contours, i, color);
//Imgproc.drawContours(drawing, hullList, i, color );
}
Note here, that I also tried using Imgproc.RETR_EXTERNAL as well, but that produced a completely black image. Also the name of the HighGui window is called "flood fill", but I just forgot to update the name.
setTo
// replace find and draw contours portion of code above
Mat out = new Mat();
background.copyTo(out);
out.setTo(new Scalar(255, 160, 130), background);
Iterating through matrix
// replace draw contours portion of code above
for (a = 0; a < background.rows(); a++) {
for(b = 0; b < background.cols(); b++) {
if(background.get(a,b)[0] == 0) {
//background.put(a, b, CvType.CV_16F, new Scalar(255, 160, 130));
double[] data = {255, 160, 130};
background.put(a, b, data);
}
}
}
The loop is promising, but I know it will not be efficient as I have 2 other masks that I would like to update as well. Could you please suggest an efficient method, that allows me to set the value for all three channels?
Thanks
I am not sure why you are doing many operations on the image but to me it looks like applying the mask and replacing the color efficiently. So if there are other complexities than please let me know.
Below is the code I was looking for in Java.
public static void main(String s[]) {
System.loadLibrary(Core.NATIVE_LIBRARY_NAME);
Mat matr =Imgcodecs.imread("/home/shariq/Desktop/test.png");
Mat result = new Mat();
//create a mask based on range
Core.inRange(matr, new Scalar(0), new Scalar(50), result);
Imgcodecs.imwrite("/home/shariq/Desktop/test_in.png", result);
//apply the mask with color you are looking for, note here scalar is in hsv
matr.setTo(new Scalar(130,160,255),result);
Imgcodecs.imwrite("/home/shariq/Desktop/result.png", matr);
}
We are creating a mask for the pixel values between 0-50 for black color using inRange method.
Core.inRange(matr, new Scalar(0), new Scalar(50), result);
This mask in result variable is than applied to original matrix using setTo method. The replacement color value is provided in HSV format through Scalar object. new Scalar(a,b,c) in HSV can be understand in RGB like this Red = c, Green = b and Blue = a.
matr.setTo(new Scalar(130,160,255),result);
Its quite fast compared to iterating the pixels one by one.
Introduction:
I'm trying to implement frustum culling and for that I created a projectionViewMatrix and then translate the vectors with the matrix. However some of the vectors seem to be incorrectly calculated. (Coordinate system: +x to the right, +y up and +z out of the screen)
Code:
public static void updateFrustum(Camera camera) {
Vector3f[] points = calculateFrustumVertices(camera);
plane[0].setPlane(points[1], points[0], points[2]);
plane[1].setPlane(points[4], points[5], points[7]);
plane[2].setPlane(points[0], points[4], points[3]);
plane[3].setPlane(points[5], points[1], points[6]);
plane[4].setPlane(points[2], points[3], points[6]);
plane[5].setPlane(points[4], points[0], points[1]);
}
private static Vector3f[] calculateFrustumVertices(Camera camera) {
// projectionMatrix was saved once at the beginning
Matrix4f inverseProjView = Matrix4f.mul(projectionMatrix, Maths.createViewMatrix(camera), null);
inverseProjView.invert();
Vector3f[] points = new Vector3f[8];
Vector4f vertex = new Vector4f();
vertex.w = 1;
for (int i = 0; i < 8; i++) {
vertex.x = clipCube[i].x;
vertex.y = clipCube[i].y;
vertex.z = clipCube[i].z;
Matrix4f.transform(inverseProjView, vertex, vertex);
vertex.x /= vertex.w;
vertex.y /= vertex.w;
vertex.z /= vertex.w;
vertex.w /= vertex.w;
points[i] = new Vector3f(vertex);
}
return points;
}
static Matrix4f viewMatrix = new Matrix4f();
public static Matrix4f createViewMatrix(Camera camera) {
viewMatrix.setIdentity();
Matrix4f.rotate((float) Math.toRadians(camera.getPitch()), Maths.xRotation, viewMatrix, viewMatrix);
Matrix4f.rotate((float) Math.toRadians(camera.getYaw()), Maths.yRotation, viewMatrix, viewMatrix);
Matrix4f.rotate((float) Math.toRadians(camera.getRoll()), Maths.zRotation, viewMatrix, viewMatrix);
Maths.reusableVector = camera.getPosition();
Maths.reusableVector2.set(-Maths.reusableVector.x, -Maths.reusableVector.y, -Maths.reusableVector.z);
Matrix4f.translate(Maths.reusableVector2, viewMatrix, viewMatrix);
return viewMatrix;
}
Example output:
For this I stand at the origin (0, 0, 0) and look in the direction of +z. My near plane is 0.001, my far plane is 1000 and the FOV is 60°. The result is (printed out each point in the for-loop in calculateFrustumVertices()):
points[0] = (0, 0, 0)
points[1] = (0, 0, 0)
points[2] = (0, 0, 0)
points[3] = (0, 0, 0)
points[4] = (1127, -591, 1110)
points[5] = (-1114, -591, 1110)
points[6] = (-1114, 668, 1110)
points[7] = (1127, 668, 1110)
Note that the first four points aren't exactly the same but due to the really small near plane distance (0.001) they almost are equal to zero. I left away the decimal places (because they're irreevant).
Problem:
Roughly the shape of the frustum is correct. But in my opinion the points are a bit wrong.
If the origin is at (0, 0, 0) shouldn't the coordinates be
symetric? So for example if the x-value of point 4 and 7 is equal to 1127,
then shouldn't the value of point 5 and 6 be eqal to -1127? (same for y and z).
(Here is a sketch for clarification) If the FOV is 60° and the far plane distance is 1000. Then in my opinion the z-value should be equal to 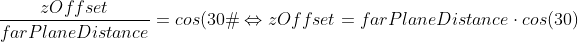 (I'm not allowed to post links, sry. Maybe someone could edit the post and get rid of the " ` " so that it's a link and not a code block. Thanks!)
If you calculate it you will get zOffset = 866. This's around 300 units smaller then the value I get with the program.
Question:
What am I doing wrong when calculating the points? The basic form is the same, but the points still differ from what they should be. Do I have a mistake somewhere? If you need more information please say so, then I will provide it.
I know this is duplicated post but still get stuck on implementation.
I following some guide on the internet in how to detect document in an image in OpenCV and Java.
The first approarch i came up with is that use the findContours after pre-process some image processing like blur, edge detection, after get all the contours i can found the largest contour and assume that is a rectangle i'm looking for but it fail in some case, e.g the document is not fully taken like missing one corner.
After trying several time and some new processing but does not work at all, i found that the HoughLine transform take it easier. From now i have all the line inside an image but still do not what to do next to defined the interest rectangle that i want.
Here is the implementation code i have so far:
Approach 1: Using findContours
Mat grayImage = new Mat();
Mat detectedEdges = new Mat();
// convert to grayscale
Imgproc.cvtColor(frame, grayImage, Imgproc.COLOR_BGR2GRAY);
// reduce noise with a 3x3 kernel
// Imgproc.blur(grayImage, detectedEdges, new Size(3, 3));
Imgproc.medianBlur(grayImage, detectedEdges, 9);
// Imgproc.equalizeHist(detectedEdges, detectedEdges);
// Imgproc.GaussianBlur(detectedEdges, detectedEdges, new Size(5, 5), 0, 0, Core.BORDER_DEFAULT);
Mat edges = new Mat();
// canny detector, with ratio of lower:upper threshold of 3:1
Imgproc.Canny(detectedEdges, edges, this.threshold.getValue(), this.threshold.getValue() * 3, 3, true);
// makes the object in white bigger
Imgproc.dilate(edges, edges, new Mat(), new Point(-1, -1), 1); // 1
Image imageToShow = Utils.mat2Image(edges);
updateImageView(cannyFrame, imageToShow);
/// Find contours
List<MatOfPoint> contours = new ArrayList<MatOfPoint>();
Imgproc.findContours(edges, contours, new Mat(), Imgproc.RETR_LIST, Imgproc.CHAIN_APPROX_SIMPLE);
// loop over the contours
MatOfPoint2f approxCurve;
double maxArea = 0;
int maxId = -1;
for (MatOfPoint contour : contours) {
MatOfPoint2f temp = new MatOfPoint2f(contour.toArray());
double area = Imgproc.contourArea(contour);
approxCurve = new MatOfPoint2f();
Imgproc.approxPolyDP(temp, approxCurve, Imgproc.arcLength(temp, true) * 0.02, true);
if (approxCurve.total() == 4 && area >= maxArea) {
double maxCosine = 0;
List<Point> curves = approxCurve.toList();
for (int j = 2; j < 5; j++) {
double cosine = Math.abs(angle(curves.get(j % 4), curves.get(j - 2), curves.get(j - 1)));
maxCosine = Math.max(maxCosine, cosine);
}
if (maxCosine < 0.3) {
maxArea = area;
maxId = contours.indexOf(contour);
}
}
}
MatOfPoint maxMatOfPoint = contours.get(maxId);
MatOfPoint2f maxMatOfPoint2f = new MatOfPoint2f(maxMatOfPoint.toArray());
RotatedRect rect = Imgproc.minAreaRect(maxMatOfPoint2f);
System.out.println("Rect angle: " + rect.angle);
Point points[] = new Point[4];
rect.points(points);
for (int i = 0; i < 4; ++i) {
Imgproc.line(frame, points[i], points[(i + 1) % 4], new Scalar(255, 255, 25), 3);
}
Mat dest = new Mat();
frame.copyTo(dest, frame);
return dest;
Apparch 2: Using HoughLine transform
// STEP 1: Edge detection
Mat grayImage = new Mat();
Mat detectedEdges = new Mat();
Vector<Point> start = new Vector<Point>();
Vector<Point> end = new Vector<Point>();
// convert to grayscale
Imgproc.cvtColor(frame, grayImage, Imgproc.COLOR_BGR2GRAY);
// reduce noise with a 3x3 kernel
// Imgproc.blur(grayImage, detectedEdges, new Size(3, 3));
Imgproc.medianBlur(grayImage, detectedEdges, 9);
// Imgproc.equalizeHist(detectedEdges, detectedEdges);
// Imgproc.GaussianBlur(detectedEdges, detectedEdges, new Size(5, 5), 0, 0, Core.BORDER_DEFAULT);
// AdaptiveThreshold -> classify as either black or white
// Imgproc.adaptiveThreshold(detectedEdges, detectedEdges, 255, Imgproc.ADAPTIVE_THRESH_MEAN_C, Imgproc.THRESH_BINARY, 5, 2);
// Imgproc.Sobel(detectedEdges, detectedEdges, -1, 1, 0);
Mat edges = new Mat();
// canny detector, with ratio of lower:upper threshold of 3:1
Imgproc.Canny(detectedEdges, edges, this.threshold.getValue(), this.threshold.getValue() * 3, 3, true);
// apply gaussian blur to smoothen lines of dots
Imgproc.GaussianBlur(edges, edges, new org.opencv.core.Size(5, 5), 5);
// makes the object in white bigger
Imgproc.dilate(edges, edges, new Mat(), new Point(-1, -1), 1); // 1
Image imageToShow = Utils.mat2Image(edges);
updateImageView(cannyFrame, imageToShow);
// STEP 2: Line detection
// Do Hough line
Mat lines = new Mat();
int minLineSize = 50;
int lineGap = 10;
Imgproc.HoughLinesP(edges, lines, 1, Math.PI / 720, (int) this.threshold.getValue(), this.minLineSize.getValue(), lineGap);
System.out.println("MinLineSize: " + this.minLineSize.getValue());
System.out.println(lines.rows());
for (int i = 0; i < lines.rows(); i++) {
double[] val = lines.get(i, 0);
Point tmpStartP = new Point(val[0], val[1]);
Point tmpEndP = new Point(val[2], val[3]);
start.add(tmpStartP);
end.add(tmpEndP);
Imgproc.line(frame, tmpStartP, tmpEndP, new Scalar(255, 255, 0), 2);
}
Mat dest = new Mat();
frame.copyTo(dest, frame);
return dest;
HoughLine result 1
HoughLine result 2
How to detect needed rectangle from HoughLine result?
Can someone give me the next step to complete the HoughLine transform approach.
Any help is appriciated. i'm stuck with this for a while.
Thanks you for reading this.
This answer is pretty much a mix of two other answers (here and here) I posted. But the pipeline I used for the other answers can be a little bit improved for your case. So I think it's worth posting a new answer.
There are many ways to achieve what you want. However, I don't think that line detection with HoughLinesP is needed here. So here is the pipeline I used on your samples:
Step 1: Detect egdes
Resize the input image if it's too large (I noticed that this pipeline works better on down scaled version of a given input image)
Blur grayscale input and detect edges with Canny filter
Step 2: Find the card's corners
Compute the contours
Sort the contours by length and only keep the largest one
Generate the convex hull of this contour
Use approxPolyDP to simplify the convex hull (this should give a quadrilateral)
Create a mask out of the approximate polygon
return the 4 points of the quadrilateral
Step 3: Homography
Use findHomography to find the affine transformation of your paper sheet (with the 4 corner points found at Step 2)
Warp the input image using the computed homography matrix
NOTE: Of course, once you have found the corners of the paper sheet on the down scaled version of the input image, you can easily compute the position of the corners on the full sized input image. This, in order to have the best resolution for the warped paper sheet.
And here is the result:
vector<Point> getQuadrilateral(Mat & grayscale, Mat& output)
{
Mat approxPoly_mask(grayscale.rows, grayscale.cols, CV_8UC1);
approxPoly_mask = Scalar(0);
vector<vector<Point>> contours;
findContours(grayscale, contours, RETR_EXTERNAL, CHAIN_APPROX_NONE);
vector<int> indices(contours.size());
iota(indices.begin(), indices.end(), 0);
sort(indices.begin(), indices.end(), [&contours](int lhs, int rhs) {
return contours[lhs].size() > contours[rhs].size();
});
/// Find the convex hull object for each contour
vector<vector<Point> >hull(1);
convexHull(Mat(contours[indices[0]]), hull[0], false);
vector<vector<Point>> polygon(1);
approxPolyDP(hull[0], polygon[0], 20, true);
drawContours(approxPoly_mask, polygon, 0, Scalar(255));
imshow("approxPoly_mask", approxPoly_mask);
if (polygon[0].size() >= 4) // we found the 4 corners
{
return(polygon[0]);
}
return(vector<Point>());
}
int main(int argc, char** argv)
{
Mat input = imread("papersheet1.JPG");
resize(input, input, Size(), 0.1, 0.1);
Mat input_grey;
cvtColor(input, input_grey, CV_BGR2GRAY);
Mat threshold1;
Mat edges;
blur(input_grey, input_grey, Size(3, 3));
Canny(input_grey, edges, 30, 100);
vector<Point> card_corners = getQuadrilateral(edges, input);
Mat warpedCard(400, 300, CV_8UC3);
if (card_corners.size() == 4)
{
Mat homography = findHomography(card_corners, vector<Point>{Point(warpedCard.cols, warpedCard.rows), Point(0, warpedCard.rows), Point(0, 0), Point(warpedCard.cols, 0)});
warpPerspective(input, warpedCard, homography, Size(warpedCard.cols, warpedCard.rows));
}
imshow("warped card", warpedCard);
imshow("edges", edges);
imshow("input", input);
waitKey(0);
return 0;
}
This is C++ code, but it shouldn't be to hard to translate into Java.
I'm working on a android application and I need to estimate online camera rotation in 3D-plan using images from camera and opencv library. I like to calculate Euler angles.
I have read this and this page and I can estimate homography matrix like here.
My first question is, should I really know the camera intrinsic matrix from camera calibrtion or is the homography matrix (camera extrinsic) enough to estimate euler angles (pitch, roll, yaw)?
If homography matrix is enough, how can I do it exactly?
Sorry, I am really beginner with opencv and cannot decompose "Mat" of homography to rotation matrix and translation matrix like describes here. How can I implement euler angles in android?
You can see my code using solvePnPRansac() and decomposeProjectionMatrix to calculate euler angles.
But it returns just a null-vector as double[] eulerArray = {0,0,0}!!! Can somebody help me?! What is wrong there?
Thank you very much for any response!
public double[] findEulerAngles(MatOfKeyPoint keypoints1, MatOfKeyPoint keypoints2, MatOfDMatch matches){
KeyPoint[] k1 = keypoints1.toArray();
KeyPoint[] k2 = keypoints2.toArray();
List<DMatch> matchesList = matches.toList();
List<KeyPoint> referenceKeypointsList = keypoints2.toList();
List<KeyPoint> sceneKeypointsList = keypoints1.toList();
// Calculate the max and min distances between keypoints.
double maxDist = 0.0;
double minDist = Double.MAX_VALUE;
for(DMatch match : matchesList) {
double dist = match.distance;
if (dist < minDist) {
minDist = dist;
}
if (dist > maxDist) {
maxDist = dist;
}
}
// Identify "good" keypoints based on match distance.
List<Point3> goodReferencePointsList = new ArrayList<Point3>();
ArrayList<Point> goodScenePointsList = new ArrayList<Point>();
double maxGoodMatchDist = 1.75 * minDist;
for(DMatch match : matchesList) {
if (match.distance < maxGoodMatchDist) {
Point kk2 = k2[match.queryIdx].pt;
Point kk1 = k1[match.trainIdx].pt;
Point3 point3 = new Point3(kk1.x, kk1.y, 0.0);
goodReferencePointsList.add(point3);
goodScenePointsList.add( kk2);
sceneKeypointsList.get(match.queryIdx).pt);
}
}
if (goodReferencePointsList.size() < 4 || goodScenePointsList.size() < 4) {
// There are too few good points to find the pose.
return;
}
MatOfPoint3f goodReferencePoints = new MatOfPoint3f();
goodReferencePoints.fromList(goodReferencePointsList);
MatOfPoint2f goodScenePoints = new MatOfPoint2f();
goodScenePoints.fromList(goodScenePointsList);
MatOfDouble mRMat = new MatOfDouble(3, 3, CvType.CV_32F);
MatOfDouble mTVec = new MatOfDouble(3, 1, CvType.CV_32F);
//TODO: solve camera intrinsic matrix
Mat intrinsics = Mat.eye(3, 3, CvType.CV_32F); // dummy camera matrix
intrinsics.put(0, 0, 400);
intrinsics.put(1, 1, 400);
intrinsics.put(0, 2, 640 / 2);
intrinsics.put(1, 2, 480 / 2);
Calib3d.solvePnPRansac(goodReferencePoints, goodScenePoints, intrinsics, new MatOfDouble(), mRMat, mTVec);
MatOfDouble rotCameraMatrix1 = new MatOfDouble(3, 1, CvType.CV_32F);
double[] rVecArray = mRMat.toArray();
// Calib3d.Rodrigues(mRMat, rotCameraMatrix1);
double[] tVecArray = mTVec.toArray();
MatOfDouble projMatrix = new MatOfDouble(3, 4, CvType.CV_32F); //projMatrix 3x4 input projection matrix P.
projMatrix.put(0, 0, rVecArray[0]);
projMatrix.put(0, 1, rVecArray[1]);
projMatrix.put(0, 2, rVecArray[2]);
projMatrix.put(0, 3, 0);
projMatrix.put(1, 0, rVecArray[3]);
projMatrix.put(1, 1, rVecArray[4]);
projMatrix.put(1, 2, rVecArray[5]);
projMatrix.put(1, 3, 0);
projMatrix.put(2, 0, rVecArray[6]);
projMatrix.put(2, 1, rVecArray[7]);
projMatrix.put(2, 2, rVecArray[8]);
projMatrix.put(2, 3, 0);
MatOfDouble cameraMatrix = new MatOfDouble(3, 3, CvType.CV_32F); //cameraMatrix Output 3x3 camera matrix K.
MatOfDouble rotMatrix = new MatOfDouble(3, 3, CvType.CV_32F); //rotMatrix Output 3x3 external rotation matrix R.
MatOfDouble transVect = new MatOfDouble(4, 1, CvType.CV_32F); //transVect Output 4x1 translation vector T.
MatOfDouble rotMatrixX = new MatOfDouble(3, 3, CvType.CV_32F); //rotMatrixX a rotMatrixX
MatOfDouble rotMatrixY = new MatOfDouble(3, 3, CvType.CV_32F); //rotMatrixY a rotMatrixY
MatOfDouble rotMatrixZ = new MatOfDouble(3, 3, CvType.CV_32F); //rotMatrixZ a rotMatrixZ
MatOfDouble eulerAngles = new MatOfDouble(3, 1, CvType.CV_32F); //eulerAngles Optional three-element vector containing three Euler angles of rotation in degrees.
Calib3d.decomposeProjectionMatrix( projMatrix,
cameraMatrix,
rotMatrix,
transVect,
rotMatrixX,
rotMatrixY,
rotMatrixZ,
eulerAngles);
double[] eulerArray = eulerAngles.toArray();
return eulerArray;
}
Homography relates images of the same planar surface, so it works only if there is a dominant plane in the image and you can find enough feature points lying on the plane in both images and successfully match them. Minimum number of matches is four and the math will work under the assumption, that the matches are 100% correct. With the help of robust estimation like RANSAC, you can get the result even if some elements in your set of feature point matches are obvious mismatches or are not placed on a plane.
For a more general case of a set of macthed features without the planarity assumption, you will need to find an essential matrix. The exact definition of the matrix can be found here. In short, it works more or less like homography - it relates corresponding points in two images. The minimum number of matches required to compute the essential matrix is five. To get the result from such a minimum sample, you need to make sure that the established matches are 100% correct. Again, robust estimation can help if there are outliers in your correspondence set -- and with automatic feature detection and matching there usually are.
OpenCV 3.0 has a function for essential matrix computation, conveniently integrated with RANSAC robust estimation. The essential matrix can be decomposed to the rotation matrix and translation vector as shown in the Wikipedia article I linked before. OpenCV 3.0 has a readily available function for this, too.
Now works the flowing code for me and I have decomposed the euler angles from homography matrix! I have some values for pitch, roll and yaw, which I don't know, whether there are correct. Have somebody any Idee, how can I test it?!
private static MatOfDMatch filterMatchesByHomography(MatOfKeyPoint keypoints1, MatOfKeyPoint keypoints2, MatOfDMatch matches){
List<Point> lp1 = new ArrayList<Point>(500);
List<Point> lp2 = new ArrayList<Point>(500);
KeyPoint[] k1 = keypoints1.toArray();
KeyPoint[] k2 = keypoints2.toArray();
List<DMatch> matchesList = matches.toList();
if (matchesList.size() < 4){
MatOfDMatch mat = new MatOfDMatch();
return mat;
}
// Add matches keypoints to new list to apply homography
for(DMatch match : matchesList){
Point kk1 = k1[match.queryIdx].pt;
Point kk2 = k2[match.trainIdx].pt;
lp1.add(kk1);
lp2.add(kk2);
}
MatOfPoint2f srcPoints = new MatOfPoint2f(lp1.toArray(new Point[0]));
MatOfPoint2f dstPoints = new MatOfPoint2f(lp2.toArray(new Point[0]));
//---------------------------------------
Mat mask = new Mat();
Mat homography = Calib3d.findHomography(srcPoints, dstPoints, Calib3d.RANSAC, 0.2, mask); // Finds a perspective transformation between two planes. ---Calib3d.LMEDS
Mat pose = cameraPoseFromHomography(homography);
//Decomposing a rotation matrix to eulerangle
pitch = Math.atan2(pose.get(2, 1)[0], pose.get(2, 2)[0]); // arctan2(r32, r33)
roll = Math.atan2(-1*pose.get(2, 0)[0], Math.sqrt( Math.pow(pose.get(2, 1)[0], 2) + Math.pow(pose.get(2, 2)[0], 2)) ); // arctan2(-r31, sqrt(r32^2 + r33^2))
yaw = Math.atan2(pose.get(2, 0)[0], pose.get(0, 0)[0]);
List<DMatch> matches_homo = new ArrayList<DMatch>();
int size = (int) mask.size().height;
for(int i = 0; i < size; i++){
if ( mask.get(i, 0)[0] == 1){
DMatch d = matchesList.get(i);
matches_homo.add(d);
}
}
MatOfDMatch mat = new MatOfDMatch();
mat.fromList(matches_homo);
return mat;
}
This is my camera pose from homography matrix (see this page too):
private static Mat cameraPoseFromHomography(Mat h) {
//Log.d("DEBUG", "cameraPoseFromHomography: homography " + matToString(h));
Mat pose = Mat.eye(3, 4, CvType.CV_32FC1); // 3x4 matrix, the camera pose
float norm1 = (float) Core.norm(h.col(0));
float norm2 = (float) Core.norm(h.col(1));
float tnorm = (norm1 + norm2) / 2.0f; // Normalization value
Mat normalizedTemp = new Mat();
Core.normalize(h.col(0), normalizedTemp);
normalizedTemp.convertTo(normalizedTemp, CvType.CV_32FC1);
normalizedTemp.copyTo(pose.col(0)); // Normalize the rotation, and copies the column to pose
Core.normalize(h.col(1), normalizedTemp);
normalizedTemp.convertTo(normalizedTemp, CvType.CV_32FC1);
normalizedTemp.copyTo(pose.col(1));// Normalize the rotation and copies the column to pose
Mat p3 = pose.col(0).cross(pose.col(1)); // Computes the cross-product of p1 and p2
p3.copyTo(pose.col(2));// Third column is the crossproduct of columns one and two
Mat temp = h.col(2);
double[] buffer = new double[3];
h.col(2).get(0, 0, buffer);
pose.put(0, 3, buffer[0] / tnorm); //vector t [R|t] is the last column of pose
pose.put(1, 3, buffer[1] / tnorm);
pose.put(2, 3, buffer[2] / tnorm);
return pose;
}