We Keep Coding

frustum for frustum culling isn't created proper

Introduction:
I'm trying to implement frustum culling and for that I created a projectionViewMatrix and then translate the vectors with the matrix. However some of the vectors seem to be incorrectly calculated. (Coordinate system: +x to the right, +y up and +z out of the screen)
Code:
public static void updateFrustum(Camera camera) {
Vector3f[] points = calculateFrustumVertices(camera);
plane[0].setPlane(points[1], points[0], points[2]);
plane[1].setPlane(points[4], points[5], points[7]);
plane[2].setPlane(points[0], points[4], points[3]);
plane[3].setPlane(points[5], points[1], points[6]);
plane[4].setPlane(points[2], points[3], points[6]);
plane[5].setPlane(points[4], points[0], points[1]);
}
private static Vector3f[] calculateFrustumVertices(Camera camera) {
// projectionMatrix was saved once at the beginning
Matrix4f inverseProjView = Matrix4f.mul(projectionMatrix, Maths.createViewMatrix(camera), null);
inverseProjView.invert();
Vector3f[] points = new Vector3f[8];
Vector4f vertex = new Vector4f();
vertex.w = 1;
for (int i = 0; i < 8; i++) {
vertex.x = clipCube[i].x;
vertex.y = clipCube[i].y;
vertex.z = clipCube[i].z;
Matrix4f.transform(inverseProjView, vertex, vertex);
vertex.x /= vertex.w;
vertex.y /= vertex.w;
vertex.z /= vertex.w;
vertex.w /= vertex.w;
points[i] = new Vector3f(vertex);
}
return points;
}
static Matrix4f viewMatrix = new Matrix4f();
public static Matrix4f createViewMatrix(Camera camera) {
viewMatrix.setIdentity();
Matrix4f.rotate((float) Math.toRadians(camera.getPitch()), Maths.xRotation, viewMatrix, viewMatrix);
Matrix4f.rotate((float) Math.toRadians(camera.getYaw()), Maths.yRotation, viewMatrix, viewMatrix);
Matrix4f.rotate((float) Math.toRadians(camera.getRoll()), Maths.zRotation, viewMatrix, viewMatrix);
Maths.reusableVector = camera.getPosition();
Maths.reusableVector2.set(-Maths.reusableVector.x, -Maths.reusableVector.y, -Maths.reusableVector.z);
Matrix4f.translate(Maths.reusableVector2, viewMatrix, viewMatrix);
return viewMatrix;
}
Example output:
For this I stand at the origin (0, 0, 0) and look in the direction of +z. My near plane is 0.001, my far plane is 1000 and the FOV is 60°. The result is (printed out each point in the for-loop in calculateFrustumVertices()):
points[0] = (0, 0, 0)
points[1] = (0, 0, 0)
points[2] = (0, 0, 0)
points[3] = (0, 0, 0)
points[4] = (1127, -591, 1110)
points[5] = (-1114, -591, 1110)
points[6] = (-1114, 668, 1110)
points[7] = (1127, 668, 1110)
Note that the first four points aren't exactly the same but due to the really small near plane distance (0.001) they almost are equal to zero. I left away the decimal places (because they're irreevant).
Problem:
Roughly the shape of the frustum is correct. But in my opinion the points are a bit wrong.
If the origin is at (0, 0, 0) shouldn't the coordinates be
symetric? So for example if the x-value of point 4 and 7 is equal to 1127,
then shouldn't the value of point 5 and 6 be eqal to -1127? (same for y and z).
(Here is a sketch for clarification) If the FOV is 60° and the far plane distance is 1000. Then in my opinion the z-value should be equal to 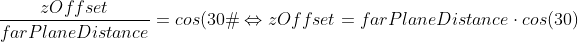![zOffset/farPlaneDist=cos(30°)](https://latex.codecogs.com/gif.latex?%5Cfrac%7BzOffset%7D%7BfarPlaneDistance%7D%20%3D%20cos%2830%B0%29%20%5CLeftrightarrow%20zOffset%20%3D%20farPlaneDistance%20%5Ccdot%20cos%2830%29) (I'm not allowed to post links, sry. Maybe someone could edit the post and get rid of the " ` " so that it's a link and not a code block. Thanks!)
If you calculate it you will get zOffset = 866. This's around 300 units smaller then the value I get with the program.
Question:
What am I doing wrong when calculating the points? The basic form is the same, but the points still differ from what they should be. Do I have a mistake somewhere? If you need more information please say so, then I will provide it.

Can't Correctly rotate 3D Point A to B (on X, Y, Z axis)

I has tirelessly been researching for three weeks now, each and every procedure for rotating a 3D Point 'A' to 3D Point 'B', the following are the techniques I attempted with no success:
Rotation Matrix
Euler Angles to Rotation Matrix
Axis Angle to Rotation Matrix
Quaternion Coordinate Rotation
Trigonometry Multiple Axis Rotation
I would like to perform a simultaneous 3d 3 axis (so, X, Y, Z) rotation in java (please know I don't particularly understand the mathematics behind it, I would prefer the answer to be in java code, with the example I displayed).
e.g.
Pointf a = new Pointf(0f, 2f, 0f);
Pointf b = new Pointf(2f, 0f, 2f);
// ~~~ Start of Rotation Matrix ~~~
// azimuth (Z Axis)
float azimuth = (float) Math.toRadians(90f);
// elevation (Y Axis)
float elevation = (float) Math.toRadians(0f);
// tilt (X Axis)
float tilt = (float) Math.toRadians(90f);
/*
public static Matrix4x4f createRotationMatrix(double azimuth, double elevation, double tilt) {
// Assuming the angles are in radians.
//Precompute sines and cosines of Euler angles
double su = sin(tilt);
double cu = cos(tilt);
double sv = sin(elevation);
double cv = cos(elevation);
double sw = sin(azimuth);
double cw = cos(azimuth);
//Create and populate RotationMatrix
Matrix4x4f A = Matrix4x4f.create();
A.values[0] = (float) (cv*cw);
A.values[1] = (float) ((su*sv*cw) - (cu*sw));
A.values[2] = (float) ((su*sw) + (cu*sv*cw));
A.values[4] = (float) (cv*sw);
A.values[5] = (float) ((cu*cw) + (su*sv*sw));
A.values[6] = (float) ((cu*sv*sw) - (su*cw));
A.values[8] = (float) -sv;
A.values[9] = (float) (su*cv);
A.values[10] = (float) (cu*cv);
return A;
}
*/
// Multiplies the Z * Y * X Rotation Matrices to form 'Matrix4x4f m'
Matrix4x4f m = Matrix4x4.createRotationMatrix(azimuth, elevation, tilt);
// Multiple point 'a' with Matrix4x4f 'm' to get point 'b'
m.transform(a); // Should return {2, 0, 2} same 'b', but returns {2, 0, 0}
// ~~~ End of Rotation Matrix ~~~
FYI. My main source of information was from the following:
http://www.euclideanspace.com/maths/geometry/rotations/conversions/angleToMatrix/index.htm
Thanks All

I can explain an algorithm for finding the matrix of rotation, though I don't have code for it.
Every rotation is around an axis. I assume that you want an axis that goes through the origin O. In that case, the rotation takes place in the plane defined by the three points O, A, and B. As the rotation axis, you can use the vector which is the cross product of the two vectors OA and OB. Here is the formula.
Let's call the three components of this direction vector for the axis (u,v,w), for simplicity (and we'll assume its normalized). Next find the angle theta between OA and OB, this is found by the standard formula for the angle between two vectors.
Finally, the hard part is done for you at this site, which links to the following 3D matrix of rotation about the origin, which will rotate A to B. Java code for this matrix can be downloaded at this site.
You can check out some rotations interactively here.

Java LWJGL OpenGL convert 3d point to 2d point

I'm trying to convert a 3d point in OpenGL to a 2d point on screen to render a healthbar for a little game I'm writing. However, I'm having some trouble retrieving the x coordinate of where to draw the healthbar. Basically, the healthbar must appear to be above a player, but must always have the same width/height relative to the screen.
I tweaked a snippet of code I found from the accepted answer at Convert a 3D location to a 2D on-screen point. (XYZ => XY) and I now have this
public static int[] getScreenCoords(double x, double y, double z) {
FloatBuffer screenCoords = BufferUtils.createFloatBuffer(4);
IntBuffer viewport = BufferUtils.createIntBuffer(16);
FloatBuffer modelView = BufferUtils.createFloatBuffer(16);
FloatBuffer projection = BufferUtils.createFloatBuffer(16);
// int[] screenCoords = new double[4];
// int[] viewport = new int[4];
// double[] modelView = new double[16];
// double[] projection = new double[16];
GL11.glGetFloat(GL11.GL_MODELVIEW_MATRIX, modelView);
GL11.glGetFloat(GL11.GL_PROJECTION_MATRIX, projection);
GL11.glGetInteger(GL11.GL_VIEWPORT, viewport);
boolean result = GLU.gluProject((float) x, (float) y, (float) z, modelView, projection, viewport, screenCoords);
if (result) {
return new int[] { (int) screenCoords.get(3), (int) screenCoords.get(1) };
}
return null;
}
It seems to work fine with the y coordinate, however, x always returns 0 no matter what the angle is.
Many thanks in advance!

screenCoords.get(3) should be screenCoords.get(0) because the x position is stored at index 0. You also only actually need the capacity of screenCoords to be 3 floats, not 4.

Generate vertices for a polygon

I'm trying to make a useful/generic 2D polygon class for an OpenGL ES renderer.
When I create a polygon, I give it several parameters:
Polygon(Vector3 centerpoint, int numVertices, float inPolySize)
Then, I try to generate the vertices. This is where i'm having a tough time. I need to determine the number of vertices, get an angle, find the x/y position of that angle, someone take the size into account, AND offset by the position.
OpenGL works with big arrays of data. Nothing is nice like Lists of Vector3's. Instead it's float[] arrays, with the first index being X1, second being Y1, third being Z1, fourth being X2, etc...
final int XPOS = 0;
final int YPOS = 1;
final int ZPOS = 2;
int mvSize = 3; // (x, y, z);
float[] vertices = new float[mvSize * mNumVertices];
for (int verticeIndex = 0; verticeIndex < mNumVertices; verticeIndex++)
{
double angle = 2 * verticeIndex * Math.PI / mNumVertices;
vertices[mvSize * verticeIndex + XPOS] = (((float)Math.cos(angle)) * mPolygonSize) + mPosition.GetX();
vertices[mvSize * verticeIndex + YPOS] = (((float)Math.sin(angle)) * mPolygonSize) + mPosition.GetY();
vertices[mvSize * verticeIndex + ZPOS] = mPolygonSize + mPosition.GetZ();
}
Unfortunatley, my triangle is never quite right. It's skewed a lot, the size doesn't seem right...
I figure i'm throwing the size into the wrong formula, can anyone help?
EDIT:
Here's some sample data
Polygon test = new Polygon( new Vector3(0, 1, 0), 3, .5f);
vertices[0] = -0.25
vertices[1] = 1.4330127
vertices[2] = 0.0
vertices[3] = -0.25
vertices[4] = 0.5669873
vertices[5] = 0.0
vertices[6] = 0.5
vertices[7] = 1.0
vertices[8] = 0.0
vertices[9] = -0.25
vertices[10] = 1.4330127
vertices[11] = 0.0

I can't believe I was this stupid. Basically, my render window was smaller than my screen. If my screen is a rectangle, my render window was a square.
This being the case, any triangle I draw that was up was clipped by my render window. To me, it looked like the triangle was skewed. Really, it was just clipped!

The Java math library takes radians as input, not degrees. I didn't see the angles you were using for your calculation, but if you're not converting to radians from degrees, you will get some skewed looking shapes, and would explain that your calculations are correct, but the expected result is off.

quaternion to angle

Alright, so this is how I am doing it:
float xrot = 0;
float yrot = 0;
float zrot = 0;
Quaternion q = new Quaternion().fromRotationMatrix(player.model.getRotation());
if (q.getW() > 1) {
q.normalizeLocal();
}
float angle = (float) (2 * Math.acos(q.getW()));
double s = Math.sqrt(1-q.getW()*q.getW());
// test to avoid divide by zero, s is always positive due to sqrt
// if s close to zero then direction of axis not important
if (s < 0.001) {
// if it is important that axis is normalised then replace with x=1; y=z=0;
xrot = q.getXf();
yrot = q.getYf();
zrot = q.getZf();
// z = q.getZ();
} else {
xrot = (float) (q.getXf() / s); // normalise axis
yrot = (float) (q.getYf() / s);
zrot = (float) (q.getZf() / s);
}
But it doesn't seem to work when I try to put it into use:
player.model.addTranslation(xrot * player.speed, 0, zrot * player.speed);
AddTranslation takes 3 numbers to move my model by than many spaces (x, y, z), but hen I give it the numbers above it doesn't move the model in the direction it has been rotated (on the XZ plane)
Why isn't this working?
Edit: new code, though it's about 45 degrees off now.
Vector3 move = new Vector3();
move = player.model.getRotation().applyPost(new Vector3(1,0,0), move);
move.multiplyLocal(-player.speed);
player.model.addTranslation(move);

xrot, yrot, and zrot define the axis of the rotation specified by the quaternion. I don't think you want to be using them in your addTranslation() call...in general, that won't have anything to do with the direction of motion.
What I mean by that is: your 3-D object -- let's say for the sake of argument that it's an airplane -- will have a certain preferred direction of motion in its original coordinate
system. So if the original orientation has the center of mass at the origin, and the
propeller somewhere along the +X axis, the plane wants to fly in the +X direction.
Now you introduce some coordinate transformation that rotates the airplane into some other orientation. That rotation is described by a rotation matrix, or equivalently, by a
quaternion. Which way does the plane want to move after the rotation?
You could find
that by taking a unit vector in the +X direction: (1.0, 0.0, 0.0), then applying the
rotation matrix or quaternion to that vector to transform it into the new coordinate
system. (Then scale it by the speed, as you're doing above.) The X, Y, and Z components
of the transformed, scaled vector give the desired incremental motion along each axis. That transformed vector is generally not going to be the rotation axis of the quaternion, and I think that's probably your problem.